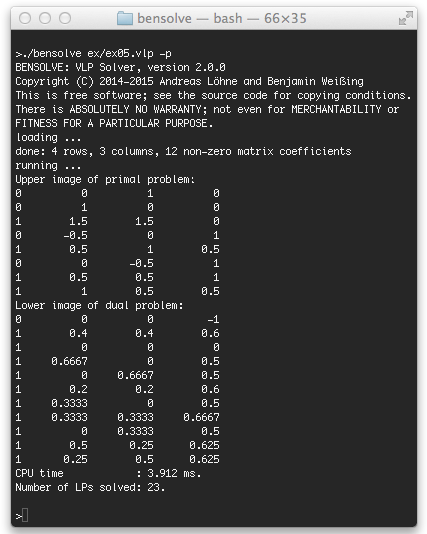
The screenshot shows output of BENSOLVE for the following very simple vector linear program:

min_C Px s.t Bx >= a, x >= 0

for

P =
    1    0    1
    1    1    0
    0    1    1
B =
    1    1    1
    1    2    2
    2    2    1
    2    1    2
a =
    1
   3/2
   3/2
   3/2

and an ordering cone C
generated by the columns of

Y =
    1     0    -1     0
    0     1     0    -1
    0     0     2     2

The output is written line-wise with a leading 0 or 1, which means that the following row vector is, respectively, a direction or a point. The points in the "Upper image of the primal problem" section are exactly the minimal (or non-dominated) vertices in the image (or outcome) space of the problem. The input of the program was read from the file "ex05.vlp" located in subdirectory "ex" (see the first line). This file has the following content:

	p vlp min 4 3 12 3 6 cone 4 6
	a 1 1 1
	a 2 1 1
	a 3 1 2
	a 4 1 2
	a 1 2 1
	a 2 2 2
	a 3 2 2
	a 4 2 1
	a 1 3 1
	a 2 3 2
	a 3 3 1
	a 4 3 2
	o 1 1 1
	o 2 1 1
	o 2 2 1
	o 3 2 1
	o 1 3 1
	o 3 3 1
	k 1 0 1
	k 2 0 1
	k 3 0 1
	k 1 1 1
	k 2 2 1
	k 1 3 -1
	k 3 3 2
	k 2 4 -1
	k 3 4 2
	i 1 l 1
	i 2 l 1.5
	i 3 l 1.5
	i 4 l 1.5
	j 1 l 0
	j 2 l 0
	j 3 l 0
	e

The input format is explained in the reference manual. It is an extension of the GLPK LP Format. It is possible to generate input files from Octave (or Matlab). Such a script is provided.

The above screenshot shows that BENSOLVE has been run with option -p. This effects output of graphics files in OFF format.

One can use, for instance, GEOMVIEW to plot this output, see www.geomview.org. We obtain the following plot of the upper image:

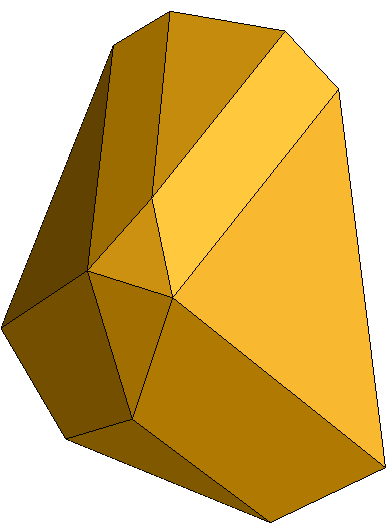
The next picture shows another variant of the 'bensolvehedron'. The feasible set of this multiple objective program is a hypercube of dimension 729 - see Example 10 in the package for q=3 and m=3. The columns of the objective matrix P are the n = (q+2*m)^q = 729 different three dimensional vectors formed by the integers -4, -3, -2, -1, 0, 1, 2, 3, 4.

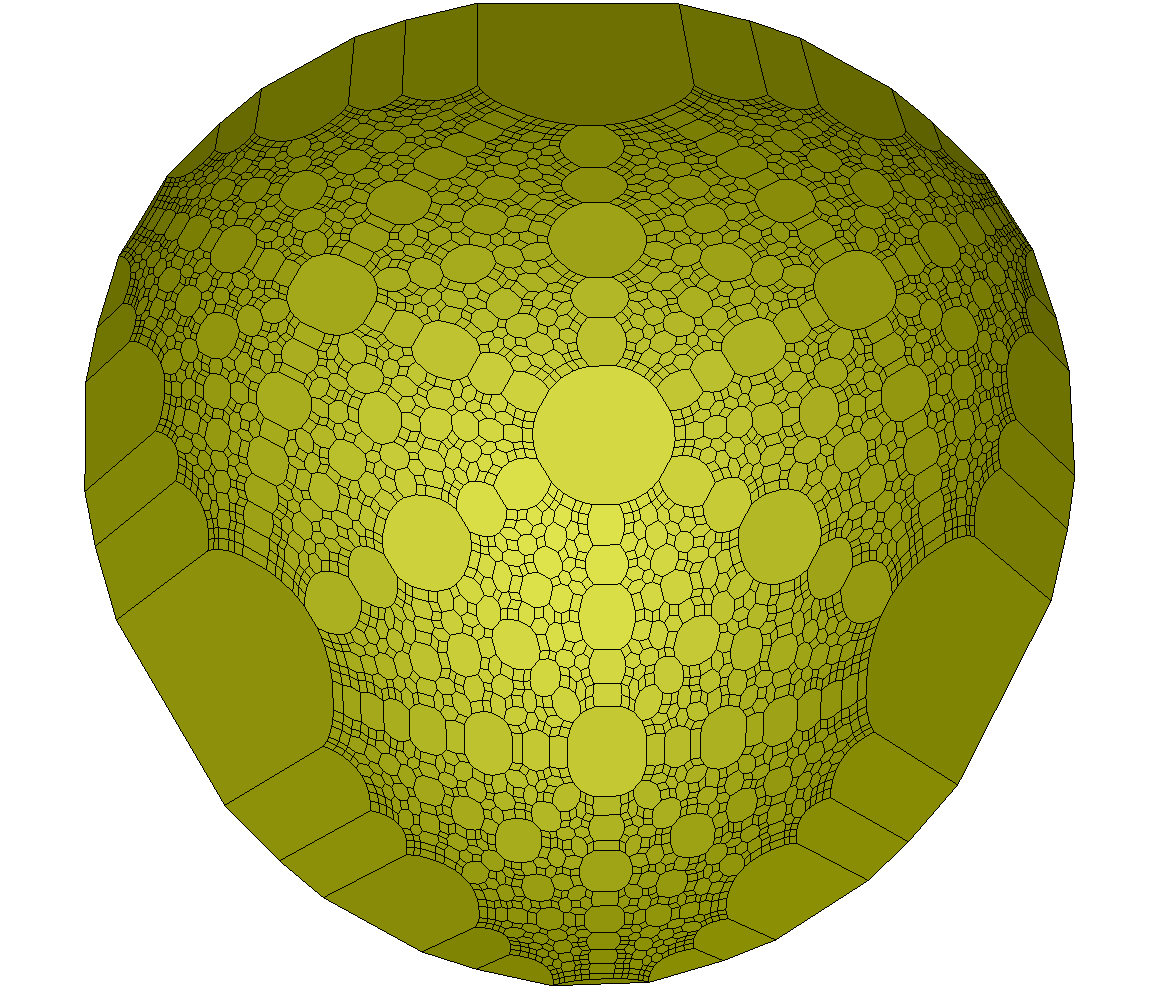
The next plot is an example by Shao and Ehrgott with 1211 constraints and 1143 variables (see ex07.vlp in the package):

For more details, see the reference manual.