Command Line

zcp Options [-Gfm] Matrix

Options: Standard options, see Standard Command Line Options

-G: Generate GAP output.

-f: Factor the polynomial.

-m: Calculate the minimal polynomial

Mat: Input matrix

Input Files

Mat: Input matrix

Description

This program reads in a square matrix and calculates its characteristic or minimal polynomial. With no options, the characteristic polynomial is computed in a partially factored form (see below). With "-m" the polynomial is split into irreducible factors. Without "-G", the output is in text format. Each line contains one factor of the characteristic or minimal polynomial. The "-G" option may be used to generate output which is readable by the GAP computer program. The output, then, is a sequence of sequences of finite field elements, representing the coefficients of the factors in ascending order.

Implementation Details

The characteristic polynomial of a matrix A is computed by constructing a sequence

$0=U_0<U_1<\ldots<U_n=V$

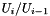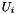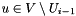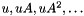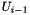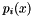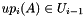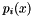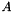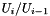of A-invariant subspaces, where $U_i/U_{i-1}$ is A-cyclic. In the i-th step, $U_i$ is constructed by chosing a random vector $u\in V\setminus U_{i-1}$ and calculating $u,uA,uA^2,\ldots$ until some linear combination of these vectors falls into $U_{i-1}$ . This yields a polynomial $p_i(x)$ with $up_i(A)\in U_{i-1}$ . is the characteristic polynomial of $A$ on $U_i/U_{i-1}$ , and the full characteristic polynomial of 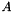$A$ is the product of all 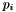$p_i$ 's.

The algorithm for the minimal polynomial uses the same technique of constructing a sequence 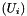$(U_i)$ of invariant subspaces. In the i-th step, images 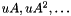$uA,uA^2,\ldots$ of a seed vector 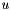$u$ are calculated, until a linear combination of these vectors vanishes (this is the main difference to the algorithm above). This yields a polynomial 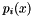$p_i(x)$ of minimal degree with 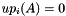$up_i(A)=0$ , and the minimal polynomial of A is the least common multiple of the 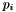$p_i$ 's.