Command Line

zts Options [-g NumGen] M N Seed [Sub]

Options: Standard options, see Standard Command Line Options

-g: Set number of generators (default is 2).

-n –no-action: Do not calculate the action of the generators on the invariant subspace. Output only the subspace.

M: First representation (left factor).

N: Second representation (right factor).

Seed: Seed vector(s).

Sub: Invariant subspace. Also used as basename for the action on the invariant subspace.

Input Files

M.1, M.2, ...: Generator action on left module. Unless changed with -g, two generators are read.

N.1, N.2, ...: Generator action on right module

Seed: Seed vector(s).

Output Files

Sub: Basis of the invariant subspace.

Sub.1, Sub.2, ...: Generator action on the invariant subspace.

See also

Description

This program is similar to zsp, but it works on the tensor product of two modules, M⊗N. zts spins up one or more vectors, and optionally calculates a matrix representation corresponding to the invariant subspace. The program does not use the matrix representation of the generators on M⊗N, which would be too large in many cases. This program is used, for example, to spin up vectors that have been uncondensed with tuc.

The action of the generators on both M and N must be given as square matrices, see "Input Files" above. You can use the -g option to specify the number of generators. The default is two generators.

Seed vectors are read from Seed. They must be given with respect to the lexicographically ordered basis explained below.

If the Sub argument is given, ZTS writes a basis of the invariant subspace to Sub, calculates the action of the generators on the invariant subspace, and writes it to Sub.1, Sub.2,...

Implementation Details

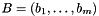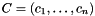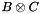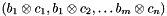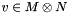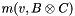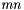Let $B=(b_1,\ldots,b_m)$ be a basis of M, $C=(c_1,\ldots,c_n)$ a basis of N, and denote by $B\otimes C$ the lexicographically ordered basis $(b_1\otimes c_1, b_1\otimes c_2, \dots b_m\otimes c_n)$ . For $v\in M\otimes N$ , the coordinate row $m(v,B\otimes C)$ has $mn$ entries which can be arranged as a 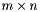$m\times n$ matrix (top to bottom, left to right). Let 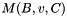$M(B,v,C)$ denote this matrix. Then

$M(B,va,C) = m(B,a|_M,B)^{\rm tr}M(B,v,C)m(C,a|_N,C) \quad\mbox{for all } a\in A,\ v\in M\otimes N$

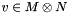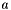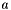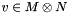Using this relation, we can calculate the image of any vector $v\in M\otimes N$ under an algebra element $a$ , and thus spin up a vector without using the matrix representation of $a$ on $v\in M\otimes N$ .