A two-level evolutionary algorithm

the upper level evolves a model structure, the lower level takes care of the parameters

Navigation

The following explanation is a snippet from

T. Lenser, T. Hinze, B. Ibrahim, P. Dittrich. "Towards Evolutionary Network Reconstruction Tools for Systems Biology"

The task of evolving an artificial CSN performing a pre-specified task can be separated into two parts: On the one hand, a set of species and reactions capable of performing that task has to be found. On the other hand, the parameters of this model structure have to be optimised for the task. The problem is thus analogue to model inference in statistics, where a set of data is used not only to fit the parameters of a model, but rather to choose a model structure together with a set of parameters. For nonlinear problems, this is still a largely unresolved challenge. Here, we show prelimininary results indicating that a separation of model-structure evolution from from parameter-fitting can help to prevent premature convergence.
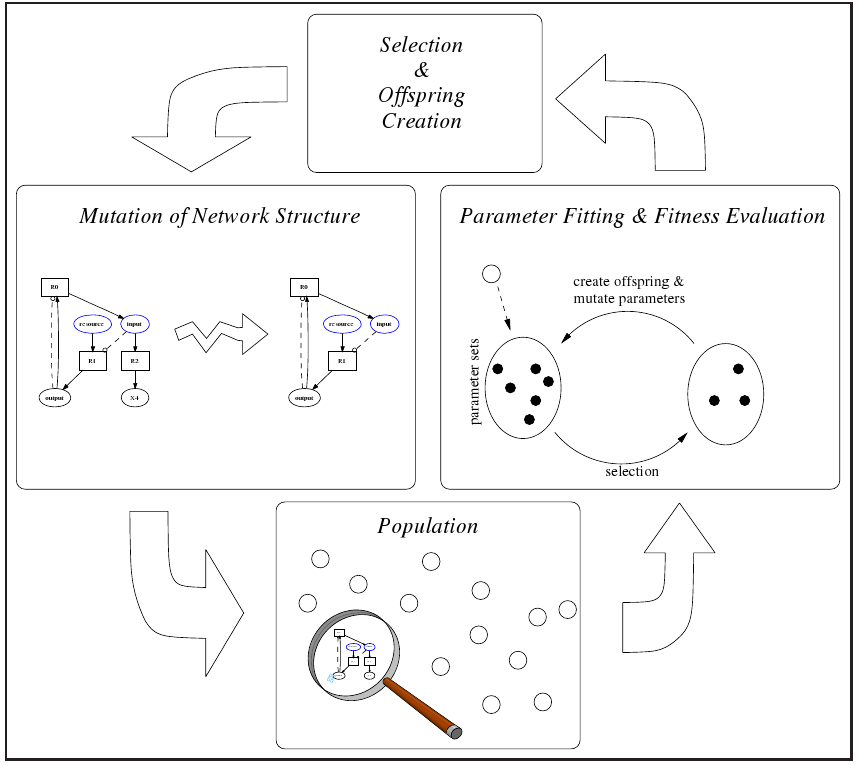
figure 7
figure 7
The question that is treated here is how much the evolution of a suitable model structure and the fitting of optimal parameters should be separated. In traditional Genetic Programming approaches, parameters are usually evolved together with the more fundamental parts. In the SBMLevolver, we provide the opportunity to clearly differentiate mutation and selection on the model structure from parameter fitting. To this end, we implemented a two-level evolutionary algorithm (figure 7), where the upper level evolves a model structure in analogy to GP, while the lower level takes care of the parameters with an evolution strategy1 approach. A similar approach has been discussed (but not implemented) for ecological models by Hoffmann 2.
In order to test the effect of this separation on the evolutionary performance, we set the task to evolve artificial CSNs which calculate the third root of a positive real number, a task which has been observed to be solvable but substantially more difficult than the evolution of a squareroot network3. We used three different parameter sets and performed nine trials for each set with and without AIC4, respectively. The parameters were chosen to represent three strategies:
  1. Two-level evolution using ES for local fitting
  2. One-level evolution running for more generations
  3. One-level evolution employing a larger population
figure 8
figure 8
Since the parameter settings were identical with respect to the number of fitness evaluations and the ratio of structural vs. parameter mutations, the one-level strategies were able to use a much larger number of generations (2) or individuals (3). The computation was carried out on a small cluster of Linux PCs. Figure 8 shows the average fitness development for each of the six cases, indicating that the use of two evolutionary levels helps to prevent premature convergence, especially in the case of an AIC-modified fitness.
1) H. Beyer and H. Schwefel. Evolution strategies, in: Natural Computing 1:3-52, 2002
2) J.P. Hoffmann. Darwin and Computational Ecology: How Simple Computational Models of Evolution Help our Search for Better Models of Ecological Systems. Proceedings of the First Open International Conference on Modeling and Simulation, Blaise Pascal University, Clermont-Ferrand, France, 2005
3) A. Deckard and H.M. Sauro. Preliminary Studies on the In Silico Evolution of Biochemical Networks. ChemBioChem 5:1423-1431, 2004
4) Akaike’s information criterion, which can be used to penalise the size of models, thus preventing overfitting