Example

In this example, the evolution of a simple network, capable of the addition of two positive real numbers, is described. The two numbers will be encoded as the initial concentrations of two input species input1 and input2, while the output of the calculation will be found in the concentration of species output at time 10.0.

As a first step, we have to prepare the building-blocks for the evolver. This is done in the file

buildingblocks.txt

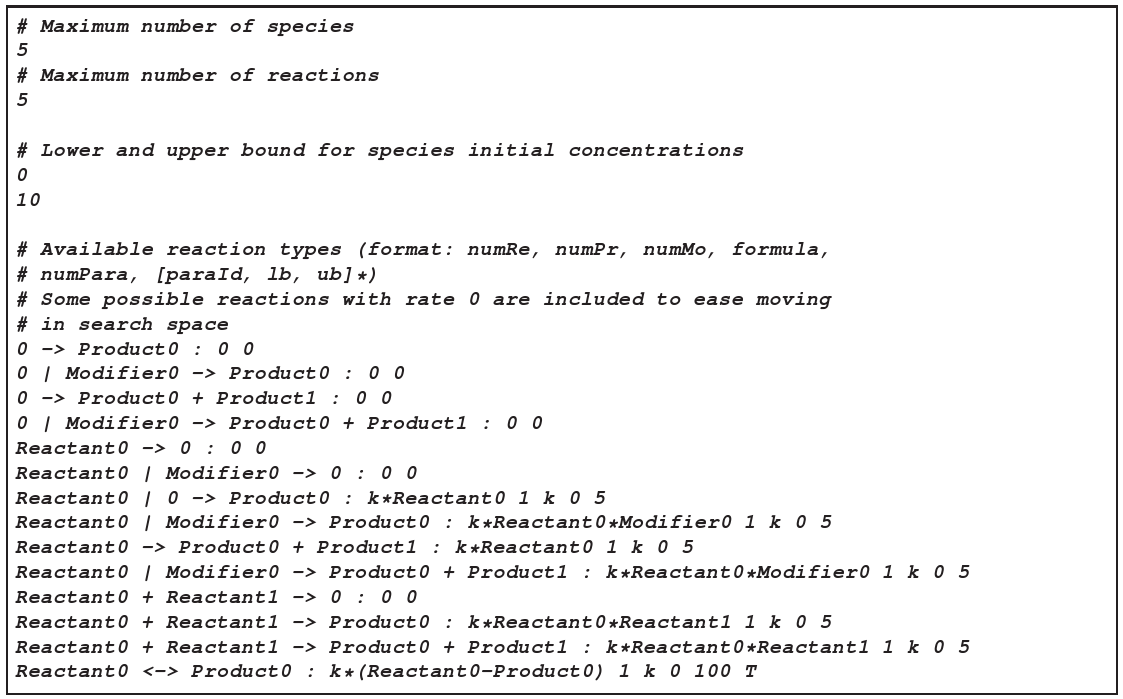
(figure 3). As you can see, we only use mass-action kinetics here. We also specify boundaries for the parameters, which helps to avoid numerical problems in the integration when the time-scales become too separated.

The second item we have to think about is the objective function (shown in figure 4). We choose to use four fitness cases, taking 0 and 10 as values for both

input1

and

input2

(more should be used, but this is not done here due to space constraints). We will measure the concentration of

output

at four timesteps of 2.0 seconds each, ignoring the first one (offset). Since the input is only to be specified at t = 0, we put a ’*’ in front of its concentration. We do not want to use Akaike’s Information Criterion to modify the fitness (

noAIC

), and we want to have a mass-conserving network (penalties for non-massconservance and size).

After the general setup of the run has been determined in the two textfiles, we have to decide about the actual parameters of the evolutionary algorithm, given in file

options.txt

(see figure 5). In this case, we choose to use a population size of 20, producing 80 offspring in a overlapping fashion, such that selection acts on 100 individuals. The population is then refilled by mutations and crossover on the survivors. All survivors are selected by elitist selection. Every tenth offspring should be produced by crossover between survivors. This is a very strong selection pressure, so it will only be successful in simple cases such as this example. In each fitness evaluation, the model parameters are be improved in a (1,5)-ES for 15 generations. Since we use default filenames for all files, we can call the SBMLevolver without command-line arguments.

The output on the screen shows best, average and worst fitness as well as average fitness-change:

The best model after this run can be seen in figure 6. By playing with the penalties and AIC, we would hope to find a more elegant solution that focuses on the bare necessities of the problem.