
|
Titel | |||

|
Grußworte
|
|||

|
Vorwort
|
|||

|
Abstracts und Personalien der Referenten |
|||

|
Beiträge | |||

|
Zur Abschluss- diskussion |
|
Friedrich-Schiller-Universität Jena
 |
 Abstract ansehen |
 pdf-Datei |
Kurzinhalt
Menschen denken, fühlen und spüren. Rechnen können wir auch, doch nicht sehr gut. Computer dagegen sind Rechengiganten, aber sie können eben nur rechnen. Durch geeignetes Kombinieren der unterschied-lichen Gaben und Stärken von Mensch und Computer sind beeindruckende Erfolge möglich.
Beim 3-Hirn-Prinzip sind ein Mensch und zwei Computer beteiligt. Auf den Computern laufen verschiedene Programme. Der Mensch läßt beide Apparate rechnen. In einem geeigneten Moment stoppt er sie, wägt ihre Lösungsvorschläge gegeneinander ab und entscheidet sich für eine der Alternativen. Der Mensch wählt also aus den Vorschlägen der Computer aus. Im Leistungsschach sind 3-Hirne, bestehend aus einem Amateurspieler und kommerzieller Software, bis in die Weltspitze vorgedrungen. Das 3-Hirn ist ein Entscheidungs-Unterstützungs-System mit Multiple Choice-Struktur. Im Vortrag werden solche Multiple Choice-Systeme vorgestellt und diskutiert.
1. Einleitung
Ein Mensch formuliert ein Problem und setzt eines oder mehrere Computerprogramme darauf an. Die Programme liefern nach Ausführung von mehr oder weniger komplexen Rechnungen eine überschaubare Handvoll von Lösungsvorschlägen. Aus dieser Kandidatenmenge trifft der Mensch die Endauswahl. Solch ein System nenne ich ein "Entscheidungs-Unterstützungs-System mit Multiple Choice-Struktur" oder kurz auch "Multiple Choice-System".
Im Schach habe ich über 13 Jahre verteilt sehr erfolgreich mit Multiple Choice-Systemen experimentiert (Althöfer 1998). Die erreichten Spielstärken lagen deutlich über den Spielstärken der beteiligten Schachcomputer und der des auswählenden Menschen. Aufgrund der beim Schach gemachten Erfahrungen glaube ich, daß Multiple Choice-Systeme auch in vielen anderen Bereichen erfolgreich eingesetzt werden können, insbesondere auch in der Mathematik.
2. Multiple Choice-Systeme im Schach
Beim 3-Hirn sind ein Mensch und zwei verschiedene "normale" Schachcomputer beteiligt. Der Mensch startet beide Apparate und ruft zu einem passenden Zeitpunkt ihre Zugvorschläge ab. Dann wählt er aus diesen beiden Vorschlägen den seiner Meinung nach besseren aus. Falls beide Computer denselben Zug vorschlagen, muß dieser ausgeführt werden. Der Mensch darf die Computer also nicht überstimmen. Das 3-Hirn spielt Schachpartien gegen andere Menschen oder Schachcomputer.
Bei Doppel-Fritz mit Boß sind ein Mensch und nur ein Schachcomputer beteiligt. Der Schachcomputer muß jedoch einen Modus haben, in dem er nicht nur den seiner Meinung nach besten, sondern auch den zweitbesten Zug ermittelt. Der Mensch wählt unter diesen zwei Zugvorschlägen des einen Programmes aus. Die Konstruktion habe ich "Doppel-Fritz mit Boß" genannt, weil das bei meinen ersten Experimenten benutzte Schachprogramm "Fritz 4" hieß. Im Unterschied zum 3-Hirn hat der Mensch also fast immer zwei Züge zur Auswahl. Das Problem war, daß oft beide Vorschläge nach Fritz "rochen".
Das Listen-3-Hirn vereinigt die Ansätze von 3-Hirn und Doppel-Fritz mit Boß. Beteiligt sind ein Mensch und zwei verschiedene Schachcomputer. Jedes Programm bestimmt zum Beispiel die seiner Meinung nach drei besten Züge. Der Mensch wählt aus den beiden Vorschlagslisten den endgültig zu spielenden Zug aus.
Mit 3-Hirnen habe ich von 1985 bis 1996 experimentiert, mit Doppel-Fritz mit Boß in der zweiten Hälfte von 1996, mit dem Listen-3-Hirn im Jahr 1997. In all diesen Experimenten war ich der auswählende Mensch. Die erreichten Spielstärken waren durchschnittlich eine ganze Klasse besser als die der benutzten Schachprogramme, und diese wiederum waren seit spätestens 1989 mindestens eine ganze Klasse besser als ich selbst. Herausragende Ereignisse waren für mich ein 5:3-Sieg über den Internationalen Meister Dr. Helmut Reefschläger Anfang 1992, eine 3,5:4,5-Niederlage gegen Großmeister Christopher Lutz 1995, ein 4,5:3,5-Sieg gegen Großmeister Genadi Timoschenko im Herbst 1996 (mit Doppel-Fritz mit Boß) und ein 5:3-Sieg über Großmeister Artur Jussupow im Shuffle-Schach im Herbst 1997 (mit Listen-3-Hirn). Einzelheiten finden sich in meinem Buch "13 Jahre 3-Hirn". Eigentlich wollte ich 1998 gegen einen Spieler aus den Top-10 der Weltrangliste antreten und nach einem erhofften Sieg für 1999 den Weltmeister herausfordern. Ein ursprünglich spielwilliger Großmeister sagte aber nach "meinem" Sieg über Jussupow ab.
Für den Erfolg des 3-Hirns und seiner Varianten sehe ich mehrere Gründe:
(a) Menschen denken und planen langfristig, machen aber viele Flüchtigkeitsfehler. Computer spielen genau, können aber nicht planen. Wählt der Mensch aus Computervorschlägen aus, so sind Flüchtigkeitsfehler fast ausgeschlossen, und der Mensch kann versuchen, seine langfristigen Pläne umzusetzen. Es werden also die Stärken von Mensch und Computern kombiniert.
(b) Ein Mensch kann berücksichtigen, gegen wen er spielt. Gegen Menschen kann der 3-Hirn-Koordinator durch seine Auswahl Stellungen anstreben, die unübersichtlich sind und beim Gegner zu Flüchtigkeitsfehlern führen. Oft habe ich im Spiel gegen Menschen nach der Maxime des früheren Vize-Weltmeisters David Bronsteins ausgewählt: "Don't solve problems, but create them." Gegen Computer kann der Koordinator Partien ruhig und mit langfristigen Plänen anlegen.
Kommerzielle Schachcomputer gibt es seit 1977. Seit einigen Jahren gibt es Schachprogramme, die nicht in erster Linie autonom spielen sollen, sondern als Analyse-Hilfen für menschliche Spieler konzipiert sind. Den Anfang machte 1993 das Programm "Doctor?", das einen K-Best-Modus hatte (Berechnung der k besten Zugvorschläge und nicht nur des besten). Vorläufiger Höhepunkt dieser Entwicklung ist das Programm "Chess-Base 7.0", unter dessen Oberfläche mehrere Schachprogramme gleichzeitig in k-Best-Modi laufen können. Abb. 1 zeigt einen Screenshot zu CB 7.0, wobei gerade die Programme Fritz 5.32 (im 2-Best-Modus), Hiarcs 7.32 (im 3-Best-Modus) und Junior 5.32 (im 3-Best-Modus) rechnen. Schön ist, daß man als Benutzer den Parameter k für verschiedene Programme verschieden setzten kann. Schön ist auch, daß man die Schriftgrößen in den Anzeigen der Programme separat wählen kann. So kann man die Vorschläge der vermeintlich wichtigeren Programme durch größere Schrift hervorheben.
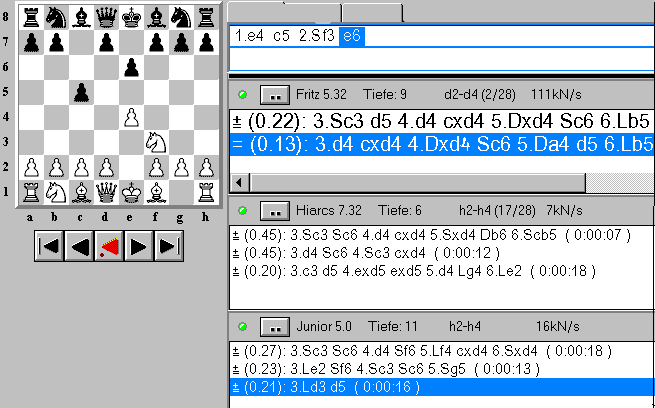
Abb. 1 Screenshot zu ChessBase 7.0
3. Beispiele zu Multiple Choice-Systemen in anderen Bereichen
In einigen anderen Bereichen sind Multiple Choice-Systeme etabliert. Dieser Abschnitt führt vier Beispiele auf.
(a) Die Firma AND hat ein Programm "FLIGHT WORLD" entwickelt, das für beliebige Flughäfen und Zeitfenster Flugverbindungen vorschlägt. Bei der Anzeige von konkurrierenden Alternativen sind diese nach ansteigender Gesamtflugzeit geordnet. So findet man typischerweise am Listenbeginn die besten Verbindungen. Abb. 2 zeigt einen Screenshot zur Verbindung "Erfurt à Hamburg".
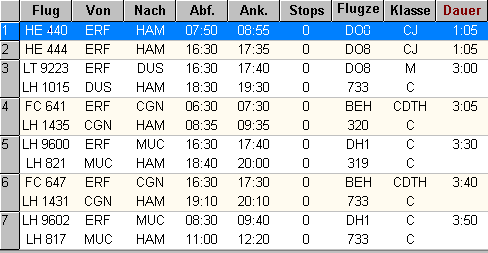
Abb. 2 Flugvorschläge für "Erfurt à Hamburg" für den 10.7.99
(b) Seit einigen Jahren gibt es Routenplaner für den Straßenverkehr. Man gibt Start- und Zielort und eventuell weitere Parameter (Zielkriterium: "kürzeste" Route oder "schnellste", ...) ein. Das Programm macht dann einen Routenvorschlag. Viele Programme verschiedener Firmen konkurrieren miteinander. Nur die von AND entwickelten Programme erlauben, neben dem Hauptvorschlag Alternativrouten (bis zu zwei) angeben zu lassen. Abb. 3 zeigt einen Screenshot zur Verbindung "Jena à Hamburg". Die "optimale" Route benutzt die A9 Richtung Berlin und wird mit 5:22 Stunden Fahrtzeit und 468,8 km Länge angegeben. Die Alternative 1 fährt über Erfurt mit 5:33 Stunden und 416,1 km. Die Alternative 2 schließlich schlägt sich durch den Ostharz, in 5:25 Stunden bei 428,4 km. Es ist übrigens bei diesem Programm keine Seltenheit, daß sich die Alternative 1 von der optimalen Route deutlicher unterscheidet als Alternative 2. Anscheinend ist das Programm angewiesen, besonders die Alternative 1 deutlich verschieden von der optimalen Route zu wählen.
(c) Die Deutsche Bahn (DB) gibt regelmäßig ihren Gesamtfahrplan als CD heraus. Abb. 4 zeigt, welche Züge das Programm für die vorgegebene Strecke "Jena à Hamburg" und ein vorgegebenes Zeitfenster ermittelt.
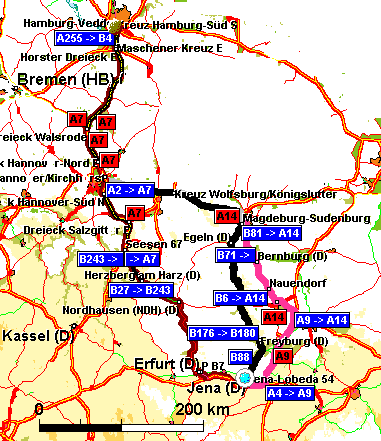
Abb. 3 Drei Vorschläge des AND-Routenplaners für "Jena à Hamburg"
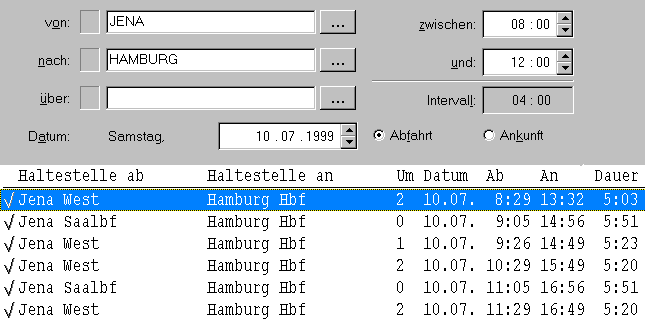
Abb. 4 Zug-Verbindungen; die Spalte "Um" gibt an, wie oft umzusteigen ist.
(d) Praktisch, aber auch ein schönes Spielzeug, ist bei der DB-CD-ROM die "phonetische Suche" nach Ortsnamen. Abb. 5 zeigt die Vorschläge des Programms, wenn man "Lalala" eingibt.
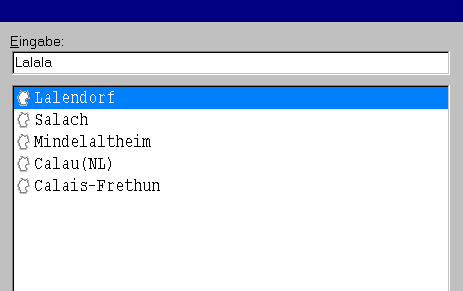
Abb. 5 Geordnete Bahnhofs-Vorschlagsliste der DB-CD-ROM zu "Lalala"
4. Visualisierung in Multiple Choice-Systemen
Eine gute Visualisierung ist bei Multiple Choice-Systemen noch viel wichtiger als bei normalen Programmen, da der auswählende Mensch statt eines Vorschlags gleichzeitig mehrere Lösungen erfassen muß. Bei z.B. drei Vorschlägen darf man nicht einfach die dreifache Datenmenge wie bei der Präsentation einer einzelnen Lösung auf den Bildschirm werfen. Auch sollten "relevante" Unterschiede der Vorschläge deutlich hervorgehoben sein, um die Auswahlentscheidung zu erleichtern. Speziell bei Systemen im Realzeit-Einsatz ist die Visualisierung wichtig, damit der auswählende Mensch nicht zur störenden Bremse wird.
5. Eine Anwendung in der mathematischen Optimierung:
Sukzessives Fixieren
In der diskreten Optimierung sind viele Probleme so schwer, daß man sie nicht in vernünftiger Zeit exakt lösen kann. Hier kommen Heuristiken zum Einsatz, etwa Greedy-Konstruktionen und Verfahren der lokalen Suche. Eine Besonderheit bei diesen typischerweise zufallsabhängigen Verfahren ist, daß sich nicht immer die gleichen guten Lösungen (z.B. lokale Optima) einstellen. So ist es etwa beim Max-SAT-Problem im 10.000-dimensionalen Hyperwürfel normal, wenn sich bei 1.000 Läufen mit lokaler Suche 1.000 verschiedene lokale Optima ergeben.
Beim sukzessiven Fixieren erzeugt man sich viele gute Lösungen und vergleicht sie miteinander. Dann entscheidet man, welche der vorkommenden Substrukturen fixiert werden sollen. (Im Hyerwürfel "{0,1} hoch n" ist etwa jede einzelne Koordinate eine solche Substruktur.) Nach dem Fixieren erzeugt man im Restproblem wieder viele gute Lösungen, inspiziert sie und fixiert weitere Teile. Nach mehreren Runden hat man schließlich alles fixiert und so eine (hoffentlich) besonders gute Lösung gefunden. Das Auswählen der zu fixierenden Teile läßt sich als Multiple Choice-Handlung realisieren.
Jochen Schoof hat in seiner Dissertation (1998) Kommunizierende genetische Algorithmen definiert und untersucht. Bei einer Variante darf der menschliche Benutzer einen genetischen Algorithmus beeinflussen, indem er "fremde" Individuen entwirft und in die Population einschleust. Die fremden Individuen lassen sich mit Hilfe eines Phänotyp-Editors entwerfen, bei dem der Mensch in Multiple-Choice-Manier wiederholt aus übersichtlichen Kandidatenmengen auswählt.
6. K-Best-Optimierung unter Nebenbedingungen
Wenn eine Aufgabe gegeben ist, bestimmt ein "normaler" Optimierungs-Algorithmus die beste Lösung. Dabei bezieht sich "beste" auf die Zielfunktion, die man für den Algorithmus formalisiert hatte. Will man mehrere Alternativlösungen bekommen, ist es naheliegend, nicht nur die beste, sondern die k besten Lösungen ermitteln zu lassen. Solche K-Best-Algorithmen werden seit Ende der fünfziger Jahre entworfen. Einen guten Überblick gibt die Internet-Bibliographie von David Eppstein. "Normale" K-Best-Algorithmen kranken bezüglich ihrer Praxisrelevanz häufig an dem Problem, daß sich die vorgeschlagenen Lösungen sehr ähnlich und dadurch keine wirklichen Alternativen sind (1. Preis: ein roter Ferrari; 2. Preis: ein roter Ferrari mit Aschenbecher).
In zwei Arbeiten mit Walter Wenzel (1999) wurde K-Best-Optimierung unter Abstandsbedingungen als Aufgabe eingeführt und exemplarisch für Matroide und ihre Verallgemeinerungen (bewertete Matroide, Delta-Matroide, bewertete Delta-Matroide) studiert: Auf dem Definitionsbereich wird eine (möglichst natürliche) Abstandsfunktion definiert, und es sind nur solche Lösungs-k-Tupel zulässig, bei denen die k einzelnen Lösungen paarweise Abstände >= d* zueinander haben. Der Parameter d* ist vom Benutzer vorzugeben. Je größer d* ist, umso verschiedener müssen die k Lösungsvorschläge sein.
7. Visionen
Auch in der symbolischen Mathematik gibt es viele Situationen, in denen Multiple Choice-Systeme Sinn machen. Bausteine für solche Systeme könnten Programme wie Mathematica, Maple und MuPAD sein.
Vielleicht werden in einigen Jahren Gruppen von nichtperfekten Theorembeweisern in Multiple Choice-Systemen sehr gute Dienste tun. Zum Beispiel war auch der ursprüngliche Beweis des 4-Farben-Satzes kein reiner Computerbeweis, sondern einer, in dem die beteiligten Menschen immer wieder Multiple Choice-Entscheidungen trafen.
Am Ende von Abschnitt 3 ging es um die "phonetische Suche" bei der DB-CD-ROM. Von der dort beschriebenen "Lalala"-Spielerei ist es nicht ganz weit zu Brainstorming-Programmen: Ein Mensch gibt Schlagwörter aus einem Problembereich in den Computer ein, und ein Programm "assoziiert" dazu andere Worte und Ausdrücke. Von Zeit zu Zeit mögen diese beim Menschen echte neue Ideen auslösen.
In der computergestützten Medizin sollte es viele Einsatzmöglichen für Multiple Choice-Systeme geben, z.B., wenn ein guter Kardiologe die Diagnosen verschiedener automatischer EKG-Analyser vergleicht.
8. Zum Recht des Überstimmens in Multiple Choice-Systemen
Oft bin ich gefragt worden, warum ich mir bei den Schach-Experimenten nicht das Recht herausgenommen hätte, die Computer zu überstimmen. Nachdem ich mich an die Koordinatorrolle gewöhnt hatte, war das fehlende Überstimmrecht sogar eine Erleichterung: Ich habe nicht dauernd nach besseren Zügen gesucht, die die Computer übersehen haben könnten, sondern mich ganz auf ihre Vorschläge verlassen. Ich kann mir jedoch vorstellen, daß eine solche Situation für Menschen mit einem sehr starken EGO schwer erträglich ist.
Bei der Deutschen Bahn werden auf einigen Strecken und Bahnhöfen neue Steuerungsstrukturen erprobt. Dazu gehört ein Computersystem, welches dem Diensthabenden Entscheidungen vorschlägt, z.B. "lasse Zug X nicht auf den verspäteten Zug Y warten". Der Fahrdienstleiter darf das Programm überstimmen. Es klappt dann aber ein Protokollfenster im Bildschirm auf, und er muß eine kurze Begründung für seine Entscheidung eintippen. Betriebsräte bei der DB haben sich jahrelang gegen diese Protokollpflicht gewehrt.
9. Faustregeln
- Kreativität im Multiple Choice-Modus ist möglich.
- Gutes Auswählen aus vorgelegten Alternativen lernt man nicht in 14 Tagen.
- Die gute Präsentation der Alternativen ist sehr wichtig.
- Die k absolut besten Lösungen bieten nicht immer die beste Auswahl. Alternativen sollten nicht nur Mikro-Mutationen voneinander sein.
Warnung: Natürlich sind Multiple Choice-Systeme nicht in jedem Problembereich der beste Ansatz!
Literatur und Software
- I. Althöfer. 13 Jahre 3-Hirn: Meine Schach-Experimente mit Mensch-Maschinen-Kombinationen. Selbstverlag, Jena 1998, ISBN 3-00-003100-6.
- I. Althöfer. Decision Support Systems with Multiple Choice Structure. Erscheint im Tagungsband "Numbers, Information, and Complexity" (Editoren I. Althöfer, N. Cai und andere). Kluwer, Amsterdam, 1999 oder 2000, S. 1-16 (?).
- I. Althöfer und W. Wenzel. 2-Best Solutions under Distance Constraints – the Model and Exemplary Results for Matroids. Advances in Applied Mathematics 22 (1999), 155-185.
- I. Althöfer und W. Wenzel. K-Best Solutions under Distance Constraints in Valuated Delta-Matroids. Advances in Applied Mathematics 22 (1999), 381-412.
- AND Software GmbH. Auto-Routenplan-Programm Route World. Karlsruhe, 1998.
- AND Software GmbH. Flugplan-Programm Flight World. Karlsruhe, 1999.
- ChessBase GmbH. Computer-Schachprogramm ChessBase 7.0. Hamburg, 1998.
- Deutsche Bahn. Elektronischer Fahrplan Deutschland und Europa. Frankfurt a. M., 1999.
- D. Eppstein. Internet-Bibliographie zu K-Best Algorithmen.
Umfang: 399 Kilo-Byte am 30. Juni 1999.
http://www.ics.uci.edu/~eppstein/bibs/kpath.bib. - J. Schoof. Kooperative Optimierung mit Kommunizierenden Genetischen Algorithmen. Dissertation, Universität Würzburg, Fakultät für Mathematik und Informatik, September 1998.
|
|
|