1.     Einleitung

Mathematiklehrer und -didaktiker haben sich schon oft darum bemüht, Elemente aus der Geschichte der Mathematik in ihre Lehrkonzepte einzubeziehen. Anekdoten sowie interessante historischen Aufgaben und Problemen sind Beispiele für derartige Elemente. Vom Mathematiker Toeplitz 1972 wurde ein Zugang zu Inhalten heutiger Mathematik vorgestellt, der sich an deren historischen Entwicklung orientiert. Man spricht auch von der historisch-genetischen Methode.

Derartige Zugänge scheinen mir in vielfältiger Weise ausbaufähig und modifizierbar.

Faßt man das Studium der Geschichte der Mathematik auch als eine motivations- und kognitionspsychologische Langzeitstudie auf, so können sich hieraus zusätzliche „Verstehensfolien" für das mathematische Denken von Schülerinnen und Schülern sowie zusätzliche Orientierungsgesichtspunkte für die Gestaltung heutigen Mathe- matikunterrichtes ergeben.
In diesem Beitrag sollen daher zwei Fragen näher untersucht werden:

(1)  Welche Motive erwiesen sich im Laufe der Geschichte immer wieder als stimulierend für die Produktion neuer Mathematik?[1]

(2)  Welche heuristischen Methoden, d. h. dem Erfinden förderliche Denkwerkzeuge, erwiesen sich in der Geschichte der Mathematik als besonders fruchtbar?

Auf diese Fragen sollen vorläufige Antworten in Form von Thesen gegeben werden, die anhand von Beispielen entwickelt bzw. gestützt werden sollen. Hierbei können aus Platzgründen die Beispiele nur genannt, aber nicht ausgeführt werden. Für Details muß auf die Literatur verwiesen werden.

Der Vorteil derartiger historischer Studien gegenüber Untersuchungen zur Motivation und zum Denken bei heutigen Schülern oder heutigen Experten scheint mir darin zu liegen, daß man über einen sehr langen Zeitraum über bereits eingetretene Effekte, über den Erfolg und die Fruchtbarkeit solcher Komponenten für die Entstehung neuer Mathematik Informationen bekommen kann. Mein Bemühen zielt daher darauf, die empirische Basis zur Untersuchung kreativer Prozesse bei mathematischen Tätigkeiten im Hinblick auf „Beobachtungszeit", „Umfang von Stichproben" aber vor allem auch im Hinblick auf „Variantenreichtum" auszuweiten.

Gegenüber normalen empirischen Untersuchungen gibt es dabei natürlich auch Einschränkungen:

1.      Z. B. sind bei derartigen Untersuchungen in natürlicher Weise die „Befragungsmöglichkeiten" beschränkt.

2.      Man ist hierbei - wie allerdings auch bei gewöhnlichen empirischen Untersuchungen - auf Interpretationen angewiesen.

Zu berücksichtigen ist auch, daß sich die Vorstellungen über Mathematik im Laufe der Zeit immer wieder geändert haben.

Angemerkt sei, daß sich schon Klix 1983 in seiner „Entwicklungsgeschichte der menschlichen Intelligenz" mit ähnlichen Fragen befaßt hat.

 

2.     Über Motive zur Herstellung neuer Mathematik

Was hat seit frühesten Zeiten Menschen motiviert, was kann sie veranlaßt haben, neue Mathematik zu erfinden?

Motiv 1: Nutzen und Anwendung

Eines der ältesten Motive zur Beschäftigung mit Mathematik ist zweifellos die Bewältigung praktischer Lebenssituationen.

Schon vor über 30000 Jahren wurden z. B. Tierknochen in Südafrika und Zentraleuropa dazu benutzt, Zahlen zu markieren, um kalendarische Daten festzuhalten oder die Anzahl erlegter Tiere zu dokumentieren[2].

Vor über 5000 Jahren entstand in Mesopoamien die Keilschrift. In dieser wurden z. B. erste Texte zur Wirtschaftsverwaltung verfaßt. In diesem Zusammenhang wurden auch Anzahlen und Mengen durch Zahlzeichen festgehalten, die sich oft je nach Bereich[3] unterschieden. Es gab für die verschiedenen Einheiten Umrechungsfaktoren wie 10; 5 und 6, worin u. a. der Beginn erster Keimzellen für Stellenwertsysteme gesehen werden kann. Es dauerte aber immerhin noch ca. 1000 Jahre, bis sich zunächst das Sexagesimalsystem in Mesopotamien durchsetzte[4].

Einige Zeit später fand in Ägypten eine ähnliche Entwicklung statt. Schon in den „Historien" von Herodot (ca. 500 v. Chr.) kann man nachlesen, daß insbesondere die jährlichen Nilüberschwemmungen[5] Anlaß gaben, z. B. intensiver über Feldaufteilungen und damit zusammenhängende Besteuerung nachzudenken. Dieses wird auch durch entsprechende Probleme im „Papyrus Rhind" deutlich[6].

Es ist klar, daß die stimulierende Wirkung lebensnaher Situationen zur Entstehung neuer Mathematik bis heute nicht an Bedeutung eingebüßt hat.

 

Motiv 2: Riten und Religionen

Seit frühester Zeit scheinen rituelle oder religiöse Motive nicht weniger wichtig für die Entstehung neuer Mathematik gewesen zu sein. In diesem Zusammenhang dürfte die neolithische Anlage von Stonehenge im Südwesten von London bekannt sein, die wahrscheinlich aus dem 3. Jahrtausend vor Chr. stammt. Dieses Monument kann interpretiert werden als geniale astronomische Kalenderanlage, die es z. B. ermöglichte, passende Zeiten für die Feldbestellung aber auch für sich jährlich wiederholende rituelle Feste vorherzubestimmen[7].

Die Tradierung von Religion wie auch von archaischer Wissenschaft durch Priesterkasten war im alten Ägypten wie auch Mesopotamien üblich[8]. Nach Schwaller de Lubicz 1962 war die alte ägyptische Mathematik primär theologisch motiviert und hatte auch noch entsprechenden Einfluß auf die folgende Zeit der Pythagoreer. Diese bildeten nach Hauser 1955 mehr als eine Schule; nämlich eine „halbreligiöse Sekte, eine Art Bruderschaft oder Orden" (S. 54).

Altarbauten zur Zeit der Veden in Indien[9] waren ein wesentliches „Stimulans" für die Entstehung von Mathematik, speziell von Geometrie.

Dieses ist insbesondere den Sulba-Sutra[10] zu entnehmen[11].

Auch beim bekannten Würfelverdopplungsproblem ging es um einen Altar, nämlich einen solchen in Delos.

Im Islam spielte ebenfalls das Betreiben von Mathematik in Zusammenhang mit der Lobpreisung von Allah eine große Rolle (bis heute!).

Im europäischen Mittelalter wurde Raimondus Lullus ohne sein Wissen zum europäischen Mitbegründer der Kombinatorik. Seine systematischen Lobpreisungen Gottes wurden nämlich für Leibniz ca. 400 Jahre später eine wesentliche Grundlage seiner „Dissertatio de arte combinatoria"[12]. Hier fand eine ähnliche Entwicklung statt wie ca. 2000 Jahre vorher in Indien. Auch in mythologischen Versen der Jaina sind mit systematischen Variationen von Textteilen Grundlagen der Kombinatorik entwickelt worden[13].

Im europäischen Mittelalter war z. B. der Kardinal Cusanus zugleich ein bekannter Mathematiker, der sich zum Zwecke eines genaueren Gottesverständnisses mit der Quadratur des Kreises beschäftigte[14]. Auch Kepler war bei seinen mathematischen Forschungen oft stark religiös motivierten. Gleiches gilt nach eigenem Bekenntnis auch noch für E. Kähler, ein bekannter zeitgenössischer Mathematiker.

 

Motiv 3: Wiederholbarkeit und Sicherheit von Rechenverfahren (Algorithmen)

Mit dem Bestreben, reale Situationen mittels Mathematik zu bewältigen, war oft das Verlangen verbunden, immer wieder vorkommende Berechnungen zu vereinheitlichen, so daß diese von möglichst vielen Nutzern beliebig oft, bequem, vielfältig und sicher eingesetzt werden können. Der Wunsch nach derartigen „Rezepten" ist sicher auch heute nicht geringer geworden. Diesen kann man sich als ein wichtiges Motiv zur Entwicklung von Algorithmen vorstellen.

Derartige z. T. recht anspruchsvolle Rechenverfahren wurden schon in Mesopotamien und im alten Ägypten entwickelt[15]. In China wurden Verfahren hervorgebracht, die z. T. in Europa erst 2000 Jahre später wiederentdeckt wurden. Am bekanntesten ist sicher der „Gauß'sche Algorithmus" zur Lösung Linearer Gleichungssysteme[16].

Diesem Verlangen nach Sicherheit, bequemer Berechenbarkeit und beliebiger Wiederholbarkeit kann heute dank Computer noch in einem viel größerem Maß entsprochen werden. Das kann allerdings dazu führen, daß man dem Computer auch ein unsinniges Resultat „glaubt", weil es ja mit präzisen Methoden zustande kam!

 

Motiv 4: „Spieltrieb"

Von alters her gehört das Spielen zu den Grundbedürfnissen der Menschen. Diese These wird z. B. durch die Tatsache gestützt, daß in Ägypten und Mesopotamien Gräbern verstorbener Herrscher nicht nur Lebensmittel und Kleidungsstücke sondern auch (Brett-)Spiele[17] beigefügt wurden. Auch Würfelspiele und Glücksspiele waren im Altertum schon bekannt.[18] Hierdurch wurde z. B. die Grundlage der Wahrscheinlichkeitsrechnung gelegt[19]. Die geometrische Wahrscheinlich­keitsrechnung wurde von Buffon in der Mitte des 18ten Jahrhunderts ebenfalls durch Probleme der Unterhaltungsmathematik begründet[20]. Die Graphentheorie entstand ungefähr zur gleichen Zeit durch das „Königsberger Brückenproblem" von Euler[21].

Gewisse Typen von Problemen der Unterhaltungsmathematik reizten über Jahrhunderte bis heute immer wieder zur Auseinandersetzung hiermit. Hierzu gehören etwa das bekannte „Problem der 100 Vögel" oder auch magische Quadrate.[22]

 

Motiv 5: Ästhetik

Auch in diesem Fall findet man schon in Zeugnisse aus Mesopotamien Verbindungen zwischen Mathematik und Kunst und damit auch ästhetische Elemente. Z. B. die Tontafel BM 15285[23] gibt Berechnungen von Flächeninhalte geometrischer Figuren wider, die viel später auch als Elemente in islamischer Kunst und Architektur - vor allem als Ornamente in Moscheen - wieder auftauchten. Beim Tempel- und Statuenbau in Ur und im alten Ägypten wurden Elemente darstellender Geometrie entwickelt[24]. Der goldene Schnitt ist wohl das seit der Antike[25] bekannteste Beispiel dafür, wie sich aus (europäischer!) Kunst und Ästhetik ein Teilstück Mathematik entwickeln kann.[26] Natürlich gibt es auch einen umgekehrten Einfluß.

Die intensive Beschäftigung mit dynamischen Systemen und fraktaler Geometrie in jüngster Zeit ist sicher zum Teil auf die in diesem Zusammenhang produzierbaren ästhetisch reizvollen Bilder zurückzuführen.

Aber auch das Streben noch Harmonie und „innerer" Schönheit ist mindestens seit der Antike ein wichtiger Antrieb zur intensiven Beschäftigung mit Mathematik[27].

 

Motiv 6: Interesse an Methoden der Erkenntnisfindung; Heuristik

Seit frühesten Zeiten wurden Entdeckungsmethoden wie „Analogisieren", „schrittweise Näherung" und „Rückwärtsarbeiten" i. a. unbewußt bei der Produktion neuer Mathematik angewandt[28].
Die bewußte und kontrollierte Verwendung derartiger heuristischer Verfahren mit dem Ziel, mathematische Erfindungen zu machen, läßt sich wiederum erstmals im griechischen Altertum nachweisen. Erste eher philosophisch motivierte Reflexionen über derartige Verfahren findet man bei Platon und Aristoteles. Von erheblich größerer mathematischer Bedeutung sind die „Methodenschrift" von Archimedes 1983a und der Band 7 der „Collectiones" von Pappos[29]. Das zuletzt genannte Werk kann als ein erstes Lehrbuch mathematischer Heuristik aufgefaßt werden. Es hatte entscheidenden Einfluß auf die Entwicklung der Mathematik vor allem bei Viète und Descartes (s. u.). Die Methodenschrift konnte vor allem deswegen nicht diesen Einfluß haben, weil sie über 2000 Jahre verschollen war und die hierin enthaltenen Ideen über „Indivisibilien" mühsam und oftmals auch weniger zweckmäßig (z. B. von Cavalieri) wiederentdeckt werden mußten. Überhaupt kann vermutet werden, daß im Altertum (z. B. auch bei Euklid) ein viel größeres Interesse an heuristischen Methoden vorlag, als man heute oftmals annimmt. Dies hat zum einen mit der Quellenlage zu tun[30], zum anderen wird unser heutiges Bild griechischer Mathematik ganz wesentlich durch die historischen Untersuchungen des letzten Jahrhunderts geprägt, in dem man vor allem an der „Grundlagenfrage" (Beginn der Axiomatik) und weniger an heuristischen Methoden interessiert war.

Ein weiteres intensives - und bislang wohl kaum bekanntes - Interesse an heuristischen Methoden ist im arabischen Sprachraum insbesondere im 10. Jahrhundert festzustellen: von Ibn al Haytham[31], Ibn Sinan[32] und al Sijzi[33] wurden ganze Lehrbücher zur mathematischen Heuristik verfaßt. Während es in den Büchern von Ibn al Haytham und Ibn Sinan vor allem um das Wechselspiel von Analysis und Synthesis geht (s. u.), hat sich al Sijzi mit über 7 verschiedenen heuristischen Strategien befaßt. Überdies hat er systematische Variationen von Problemen vorgenommen und diese zu ganzen Problemfeldern ausgeweitet[34], eine ganz aktuelle Thematik in Zusammenhang mit der Diskussion über eine „bessere Unterrichtskultur", die sich an TIMSS anschloß.

In der Renaissance kam es auch zu einer sehr eindrucksvollen „Wiedergeburt" des Interesses an (nicht nur mathematischer) Heuristik. Viète, Descartes und Leibniz sind wohl die bekanntesten unter den zahlreichen Personen dieser Zeit, die sich um umfassende Methoden zum Erfinden und Urteilen bemühten („ars inveniendi et judicandi"). Wie weit tatsächlich der Anspruch dieser Autoren ging, wird durch folgende Äußerungen von Viète deutlich: „Schließlich nimmt die analytische Kunst ... mit Recht das berühmte Problem der Probleme für sich in Anspruch, das ist: Kein Problem ungelöst zu lassen."[35]

Einen ähnlichen Anspruch verfolgte Descartes mit seiner „Méthode" und seinen „Regulae ad directionem ingenii"[36]. Gleiches gilt auch für das Anliegen von Leibniz, eine „characteristica universalis" zu entwickeln.

Viète und Descartes knüpften in besonderem Maße an die erwähnte Arbeit von Pappos an und kamen so zu neuen mathematischen Erkentnissen und Methoden (von der Buchstabenalgebra zur „analytischen Geometrie"). Leibniz entwickelte u. a. in seiner Schrift „De la Sagesse"[37] die „Méthode" von Descartes weiter und vor allem mit seinem Differential- und Integralkalkül eine sehr elegante und effektive „lokale" Lösung seines Strebens nach einer characteristica universalis. Auch E. Weigel, zeitweise der Lehrer von Leibniz an der Universität Jena, fühlte sich diesem Zeitgeist verbunden[38].

Wenn auch Viète, Descartes und Leibniz mit ihrem umfassenden Anspruch nicht erreichbare Ziele verfolgten, so kann festgehalten werden, daß doch dieser sie zu wesentlichen produktiven mathematischen Beiträgen antrieb.

Ähnliches läßt sich über die Entwicklung der künstlichen Intelligenz mit Beginn der fünfziger Jahre dieses Jahrhunderts sagen:

So war es natürlich nicht möglich, einen „general problem solver"[39] zu entwickeln. Doch auch hier hat dieses hochgesteckte Ziel oftmals zu sehr brauchbaren lokalen Lösungen (Expertensystemen) geführt.

 

Motiv 7: Interesse an Methoden der Erkenntnissicherung;Beweise

Das Streben nach Sicherheit mathematischer Erkenntnis und nach stichhaltigen Begründungen zeichnete die griechische Antike vor den mathematischen Betätigungen in anderen Kulturkreisen aus. Die „Elemente" von Euklid und die Arbeiten von Archimedes werden hierfür oft als repräsentativ angesehen. Sie prägten wesentlich mit den Stil heutiger mathematischer Arbeit

Das Interesse an Begründungen war bei verschiedenen Völkern und zu verschiedenen Zeiten unterschiedlich.

So findet man z. B. in den chinesischen „9 Büchern der arithmetischen Technik" keinen einzigen Beweis. Hieraus kann aber nicht geschlossen werden, daß zu dieser Zeit (ca. 150 v. Chr.) in China Beweise keine Rolle spielten, denn über die Funktion dieses Buches sowie über mögliche Formen mündlicher Behandlung von Mathematik wird hierin nichts gesagt.

Einige Zeit später (ca. 250 n. Chr.) wurden von Liu Hui, einem Kommentator dieser Schrift, Begründungen zu hierin enthaltenen Aussagen in Form geometrischer Arrangements gegeben („Tangram-Beweise").

Bei den Veden in Indien waren Beweisformen stark mit religiösen Riten verzahnt, die wiederum mit Symmetrieprinzipien und Handwerklichen Tätigkeiten verbunden waren.[40]

In der Renaissance gab es z. B. bei de Vincento ein Beweisverständnis, das eine Kette fortschreitender Verallgemeinerungen für Begründungen eines zunächst an einem Spezialfall beobachteten Sachverhaltes umfaßte.[41]

Mit Beginn des letzten Jahrhunderts brachte die „Grundlagenkrise" der Mathematik über Boole, Frege, Russel, Hilbert bis Gödel erhebliche Fortschritte auf Seiten der Absicherung mathematischer Erkenntnisse. Dabei wurden auch mathematische Logik weiterentwickelt. Hierzu kann auch die Tatsache gerechnet werden, daß von Gödel[42] mit Hilfe von Logik ihre Grenzen aufgezeigt wurden. Indirekt kann hierin eine Rechtfertigung für eine Betonung der Wichtigkeit heuristischer Verfahren gesehen werden.

In jüngster Zeit wurden wesentliche Teile von Beweisen mit Computerhilfe durchgeführt (z. b. beim Vier-Farben-Problem und der Klassifikation einfacher Gruppen).

 

Motiv 8: Interesse an Systemen und Theorien

Von Euklid bis Bourbaki war es immer wieder ein längerfristiges Ziel vieler Mathematiker, ihre Ergebnisse in umfassende möglichst axiomatisch aufgebaute Systeme einzuordnen[43]. Logik, Einfachheit und Klarheit sind hierbei wesentliche „Steuerungselemente".

Schon die vorangegangenen Überlegungen zeigen, daß es auch andere Ordnungsprinzipien mathematischer Erkenntnisse gibt: so kann man bei den Veden von einer dominierenden religiösen z. T. auch literarischen und bei dem durch die „Neun Bücher arithmetischer Technik" vermittelten Bild von einer „induktiven"[44] Ordnung sprechen.

 

Motiv 9: Interesse an herausfordernden Problemen

Herausfordernde Probleme gaben immer wieder Gelegenheit, Ehrgeiz, Stolz und das Streben nach Anerkennung von Mathematikern auf die Probe zu stellen oder in manchen Fällen auch zu befriedigen. Hierzu gehören die drei klassischen Probleme Kreisquadratur, Würfelverdopplung und Winkeldreiteilung der Antike. Hierbei erwies es sich sogar als glückliche Fügung, daß gerade diese Probleme in ihrer ursprünglichen Form (Konstruktionen mit Zirkel und Lineal) sich als nicht lösbar erwiesen. So wurden über Jahrtausende zwar nicht diese Probleme gelöst bzw. letztlich als nicht lösbar nachgewiesen, aber es wurden im Rahmen von Lösungsbemühungen Lösungen für ander oder verwandte Probleme gefunden. So wäre wohl z. B. ohne die Herausforderung durch die Quadraturproblematik kaum die Integralrechnung entstanden.

Entsprechendes gilt für das heute weniger bekannte von Pappos erwähnte[45] „Vier-Linien-Problem" von Aristaeos und Apollonios, was nach ca. 2000 Jahren von Descartes[46] gelöst wurde und damit seinen Ruhm wesentlich mit begründete. Hiermit wurde aber bekanntlich auch die „analytische" Geometrie und u. a. die Theorie der algebraischen Kurven begründet. Auch die umfangreichen Bemühung um die Lösung des Vierfarbenproblems (z. B. von Heesch), die schließlich Appel und Haken 1976[47] gelang, brachte in der Graphentheorie große Fortschritte. Entsprechendes gilt für das Fermatproblem, das über 350 Jahre mathematische Kreativität stimuliert und das jüngst im wesentlichen von Wiles[48] gelöst wurde.

 

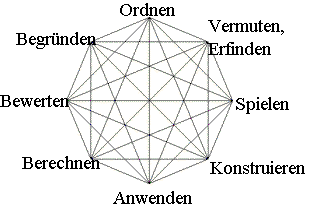
Mögliche didaktische Konsequenzen Diese Motive können zu nebenstehendem Verbund von mathematischen Tätigkeiten von Schüler führen, von dem man sich eine Förderung ihrer Kreativität erhoffen kann. Im schulischen Bereich dominiert oft das Berechnen. Auch das Anwenden und das Konstruieren findet sicher oft Berücksichtigung. An der Universität stehen sicher „offiziell" das Begründen und Ordnen im Vordergrund. Dieses Netz von Tätigkeiten kann vielleicht auch einen möglichen umfassenderen und „ausgewogeneren" Orientierungsrahmen für die Auswahl geeigneter Probleme für Schüler geben.

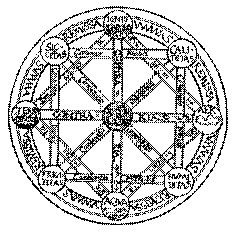
Es kann zugleich an das Logo des Symposiums erinnern. Es steht am Anfang der Leibnizschen „Dissertatio de arte combinatoria". Kombinatorik ist für Leibniz auch eine sehr wichtige Form der Kreativität, nämlich „die Kunst, Fragen zu finden"[49]. Insofern kann in diesem Zeichen auch ein Sinnbild für Kreativität gesehen werden. Es entstammt einer Schrift von Clavius aus dem Jahre 1585 und soll Teile der Aristotelischen Philosophie veranschaulichen[50].

 

 

3.     Über besonders erfolgreiche Denkwerkzeuge für die Herstellung neuer Mathematik

Pólya kommt das Verdienst zu, in neuerer Zeit die grundsätzliche Bedeutung mathematischer Heuristik für das Lösen von Problem hervorgehoben und dazu vorbildliche Beispiele und auch sehr interessante theoretische Überlegungen[51] vorgestellt zu haben.[52]

Die Bedeutung und der Stellenwert heuristischer Methoden, wie sie sich etwa anhand ihrer jeweiligen Wirkung und Fruchtbarkeit (=Potential, „neue" Mathematik zu erzeugen) über 5000 Jahre in der Geschichte der Mathematik äußert, wurde von ihm nicht untersucht.

Von herausragender Bedeutung in diesem Sinne („Invarianten"[53] bezgl. ihrer hohen Fruchtbarkeit) sind insbesondere:

Analogisieren, Rückwärtsarbeiten (die klassische analytische Methode), induktives Vorgehen, Methoden der schrittweisen Näherung (sukzessive Approximation), Repräsentations(Modalitäts-)wechsel und Indivisibilienmethoden[54].

Aus Platzgründen kann hier nur exemplarisch kurz auf die analytische Methode eingegangen werden.

Sie ist als „Analysis" seit dem griechischen Altertum bekannt[55]. Sie läßt sich wie folgt grob charakterisieren:

Man geht von der Annahme aus, daß Problem sei gelöst, der zu beweisende Satz sei wahr. Sodann werden aus dieser Annahme schrittweise Schlußfolgerungen gezogen bzw. es werden verifizierte oder verifizierbare Voraussetzungen gesucht, aus denen das jeweils Angenommene gefolgert werden könnte. Dieses geschieht so lange, bis man bei einer gesicherten Voraussetzung, etwas Gegebenem angelangt ist oder aber bei einem Widerspruch („reductio ad absurdum"), was die Unrichtigkeit der Ausgangsannahme ergibt.

Bei diesem „rückwärtigem Voranschreiten" stößt man oftmals - ggf. auch durch Widersprüchlichkeiten - auf zusätzliche Bedingungen oder Voraussetzungen, die erfüllt sein müssen (die Griechen sprachen von „Diorismen"[56]), damit das Problem lösbar oder der Satz beweisbar wird.

Hieran schließt sich - falls kein Widerspruch aufgetreten ist bzw. die Voraussetzungen geeignet modifiziert wurden - die Synthesis, d. h. der Beweis oder die Konstruktion an, wobei von Voraussetzungen zur Behauptung, von Gegebenem zu Gesuchtem vorangeschritten wird.

Auch in diesem Fall wurde schon in Mesopotamien implizit diese Methode z. B. beim Lösen quadratischer Gleichungen verwendet, die wir heute z. B in der Form x²+x=3/4 schreiben würden.[57]

In der griechischen Antike wurde dann diese Methode in verschiedener Weise von Aristaeos, Platon, Euklid, Apollonios, Archimedes, Heron und vor allem sehr folgenreich von Pappos eingesetzt und weiterentwickelt.

In den erwähnten Lehrbüchern zur Heuristik von al Haitham, Ibn Sinan und al Sijzi spielte die Analysis eine zentrale Rolle.

Gleiches gilt für die schon erwähnten Arbeiten von Viète, Descartes und Leibniz, die ganz wesentlich an die „analytische" Arbeit von Pappos anschlossen. Bei Leibniz findet man außer der oben erwähnten noch mindestens 13 weitere Verstehensweisen des Begriffes „Analysis"[58].

Die Bedeutung dieser Methode kann man auch daran erkennen, daß auch heute noch ganz Gebiete hiernach benannt sind.[59]

Auch das „backtracking" in der Informatik kann als Variante der analytischen Methode gesehen werden.

 

Welche didaktische Konsequenzen können sich hieraus ergeben?

·         Man kann an eine stärkere Akzentuierungen heuristischer Methoden wie z. B. „Analysis" und „Analogie" im Mathematikunterricht und in der Lehrerausbildung durch Auswahl hierzu passender Aufgaben und Probleme denken, die überdies auch noch mit adäquater Häufigkeit im Unterricht einzusetzen wären.

·         Es sollte überlegt werden, an welchen Stellen im Unterricht und zu welcher Zeit in der Entwicklung der Schüler solche heuristische Methoden bewußtgemacht werden können oder sollten.

·         Die Schüler sollten bei passender Gelegenheit über Zusammenhänge zwischen Heuristik und Logik nachdenken.

 

4.     Rück- und Ausblick

„Der Nutzen der Geschichte der Mathematik ergibt sich nicht nur daraus, daß die zur Mathematik Beitragenden gewürdigt werden und andere später ähnliche Anerkennung erfahren können, sondern ebenso daraus, daß die Kunst des Entdeckens und das methodische Wissen durch prägnante Beispiele gefördert wird.[60]"

Beispiele konnten hier aus Platzgründen nur genannt, aber nicht ausgeführt werden. Die Literaturverweise ermöglichen vielleicht weitergehende Studien.

Im übrigen sehe ich alle anderen Beiträge in diesem Band in ähnlicher Funktion wie die von Leibniz gemeinten.

 

Literatur

Appel, K.; Haken, W.: The Four-Color Problem. In: Steen 1979.

Archimedes: Werke: im Anh.: Kreismessung, übers. von F. Rudio; Des Archimedes Methodenlehre von den mechanischen Lehrsätzen, übers. von J. L. Heiberg und kommentiert von H. G. Zeuthen/Archimedes. Übersetzt und mit Anmerkungen versehen von A. Czwalina. Sonderausg., 4. unveränd. reprograf. Nach­druck. Wissenschaftliche Buchgesellschaft, Darmstadt 1983.

Archimedes (1983a): Des Archimedes Methodenlehre von den mechanischen Lehrsätzen, an Eratosthenes. Übersetzt von J. L. Heiberg und kommentiert von H. G. Zeuthen. In: Archimedes 1983.

Aristoteles: Nikomachische Ethik. Übersetzt und mit einer Einleitung und Anmerkungen versehen von O. Gigon. Artemis, Zürich 1967.

Bellosta, H.: ibn al Haitham: On Analysis and Synthesis. In: Arabic Sciences and Philosophy, vol. I (1991), pp. 211 - 232.

Brentjes, S.; Zimmermann, B.: Heuristisches Denken in den geometrischen Schriften von Abu Said Ahmad b. M. b. 'Abd al-Jalil al-Sijzi (2. Hälfte 10. Jh.). In: Der Mathematikunterricht 1, 1999, S. 61 - 75.

Cantor, M.: Vorlesungen über Geschichte der Mathematik. Dritter Band. B. G. Teubner, Leipzig ca. 1910.

Chabert, J.-L.; Barbin, E.; Guillemot, M.; Michel-Pajus, A.; Borowczyk, J.; Djebbar, A.; Martzloff, J.-C.: Histoire d'algorithmes. Du caillou à la puce. Belin, Paris 1994.

Chace, A. B.: The Rhind Mathematical Papyrus. Reston, NCTM 1986².

Descartes, R.: Geometrie. Deutsch herausgegeben von L. Schlesinger. Wissenschaftliche Buchgesellschaft, Darmstadt 1969.

Descartes, R.: Regulae ad directionem ingenii. Regeln zur Ausrichtung der Erkenntniskraft. Lateinisch-Deutsch. Kritisch revidiert, übersetzt und herausgegeben von H. Springmeyer, L. Gäbe, H. G. Zekel. Meiner, Hamburg 1973.

Descartes, R.: Ausgewählte Schriften. Hrsg. I. Frenzel. Fischer TB 6549, Frankfurt 1986.

Dhombres, J.: Is One Proof Enough? Travels with a Mathematician of the Baroque Period. In: Educational Studies in Mathematics 24: 401 - 419, 1993.

Euklid: Die Elemente. Nach Heibergs Text aus dem Griechischen übersetzt und herausgegeben von C. Thaer. Reprografischer Nachdruck folgender Nummern aus «Ostwald's Klassikern der exakten Wissenschaften»: Nr. 235 (Buch I - III), Leipzig 1933; Nr. 236 (Buch IV - VI), Leipzig 1933; Nr. 240 (Buch VII - IX), Leipzig 1935; Nr. 241 (Buch X), Leipzig 1936; Nr. 243 (Buch XI - XIII), Leipzig 1937. Wissenschaftliche Buchgesellschaft, Darmstadt 1980.

Fittà, M.: Spiele und Spielzeug in der Antike. Unterhaltung und Vergnügen im Altertum. Wissenschaftliche Buchgesellschaft, Darmstadt 1998.

Gerhardt, C. J. (Hrsg.): Leibnizens mathematische Schriften. Band V. H. W. Schmidt, Halle 1858. Zweiter reprografischer Nachdruck erschienen bei Olms, Hildesheim - New York 1971.

Gerhardt, C. J. (Hrsg.): Die Philosophischen Schriften von Gottfried Wil­helm Leibniz. Vierter Band. Weidmannsche Buchhandlung, Berlin 1880. Als Nachdruck erschienen bei Olms, Hildesheim - New York 1978.

Gerhardt, C. J. (Hrsg.): Die Philosophischen Schriften von Gottfried Wilhelm Leibniz. Siebenter Band. Weidmannsche Buchhandlung, Berlin 1890. Als Nachdruck erschienen bei G. Olms, Hildesheim - New York 1978.

Glatfeld, M. (Hrsg.): Finden, Erfinden, Lernen. Zum Umgang mit Mathematik unter heuristischem Aspekt. Peter Lang, Frankfurt a. M., Bern, New York, Paris 1990.

Hauser, G.: Geometrie der Griechen von Thales bis Euklid. Verlegt bei Eugen Haag in Luzern 1955.

Hawkins, G. S.: Stonehenge Decoded. An Astronomer examines one of the great Puzzles of the Ancient World. Barnes&Noble Books, New York 1993.

Herodot: Historien. Erster Band Bücher  I - V. Griechisch - deutsch herausgegeben von Josef Feix. Artemis Verlag, München und Zürich 1988⁴.

Hogendijk, J. P.: Al-Sijzi´s Treaties on Geometrical Problem Solving. Fatemi Publishing Co. Tehran 1996.

Høyrup, J.: In Measure, Number, and Weight. Studies in Mathematics and Culture. State University of New York Press, Albany 1994.

Ibn al Haitham: Kitab at-tahlil wa-t-tarkib. Ouvrage d'al-H,.asan ibn al al-H,.asan ibn al-Haitham sur l'analyse et la synthèse. Manuskript einer noch nicht veröffentlichten Übersetzung aus dem Arabischen ins Französische von K. Jaouiche et. al., Paris 1991. Verwendung mit freundlicher Erlaubnis der Autoren. Siehe auch Sezgin 1974, S. 369, Nr. 17.

Jones, A. (Hrsg. u. Übers.): Pappus of Alexandria. Book 7 of the Collection. Part 1 + Part 2. Springer, New York 1986.

Joseph, G. G.: The Crest of the Peacock. Non-European Roots of Mathematics. Penguin Books, London 1991.

Kaderávek, F.: Geometrie und Kunst in früherer Zeit. Nach dem 1935 in Prag erschienenen Original aus dem Tschechischen übersetzt von Leo Bocek und Zbynek Nádeník. Herausgegeben und mit Anmerkungen versehen von Zbynek Nádeník und Peter Schreiber. Teubner, Stuttgart-Leipzig sowie Verlag der Fachvereine, Zürich 1992.

Klix, F.: Erwachendes Denken. Eine Entwicklungsgeschichte der menschlichen Intelligenz. 2., überarbeitete und erweiterte Auflage. VEB Deutscher Verlag der Wissenschaften Berlin 1983.

Knobloch, E.: Zur Herkunft und weiteren Verbreitung des Emblems in der Leibnizschen Dissertatio de de arte combinatoria. In: studia leibnitiana, Band III Heft 4 1971, S. 290 - 292.

von Kues, N.: Die mathematischen Schriften. Übersetzt von Josepha Hofmann mit einer Einführung und Anmerkungen versehen von Joseph Ehrenfried Hofmann. Felix Meiner, Hamburg 1979².

Leibniz, G. W.: Sämtliche Schriften und Briefe, hrsg. von der Akademie der Wissenschaften der DDR. Reihe 6: Philosophische Schriften, Band 3. Akademie Verlag, Berlin 1980.

Michaels, A.: Beweisverfahren in der vedischen Sakralgeometrie. Ein Beitrag zur Entstehungsgeschichte von Wissenschaft. Alt- und Neu-Indische Studien herausgegeben vom Seminar für Kultur und Geschichte Indiens an der Universität Hamburg. 20. Franz Steiner, Wiesbaden 1978.

Mydorge, C.: Examen du livre des Recreation Mathematiques & de ses Problemes en Geometrie, Mechaniques, Optique, & Catoptrique. Antoine Robinot, Paris 1639.

Neugebauer, O. (Hrsg. u. Übers.): Mathematische Keilschrift-Texte. Erster Teil. Texte. J. Springer, Berlin 1935.

Newell, A.; Simon, H. A.: Human Problem Solving. Prentice Hall, Englewood Cliffs 1972.

Nissen, H. J.; Damerow, P.; Englund, R. K.: Frühe Schriften und Techni­ken der Wirtschaftsverwaltung im alten Orient. Informationsspeicherung und -verarbeitung vor 5000 Jahren. Franzbecker und Max-Planck-Institut für Bildungsforschung, Bad Salzdetfurth, 1991².

Pfeiffer, X.: Der goldene Schnitt und dessen Erscheinungsformen in Mathematik, Natur und Kunst. 1885. Unveränderter Nachdruck, Sändig Reprint, Vaduz 1992.

Pólya, G.: Mathematik und plausibles Schließen. Band 1. Induktion und Analogie in der Mathematik. Birkhäuser, Basel - Boston - Stuttgart 1969².

Pólya, G.: Mathematik und plausibles Schließen. Band 2. Typen und Strukturen plausibler Folgerungen. Birkhäuser, Basel - Boston - Stuttgart 1963.

Schneider, I. (Hrsg.): Die Entwicklung der Wahrscheinlichkeits­theorie von den Anfängen bis 1933. Wissenschaftliche Buch­gesellschaft, Darmstadt 1988.

Schwaller de Lubicz, A.: De la Mathématique pharaonique. In: Chronique d' Égypte. Bulletin Périodique de la Fondation Egyptologie Reine Elisabeth. Tome XXXVII, No. 73 - Janvier 1962, S. 77 - 106.

Seidenberg, A.: Ritual Origin of Geometry. In: Archive for History of Exact Sciences. Vol. 1, 1962, S. 488 - 527.

Sezgin, F.: Geschichte des Arabischen Schrifttums. Band V. Mathematik. E. J. Brill, Leiden 1974.

Singh, S.: Fermats letzter Satz. Die abenteuerliche Geschichte eines mathematischen Rätsels. Hanser, München Wien 1998.

Srinivasiengar, C. N.: The History of Ancient Indian Mathematics. World Press, Calcutta 1988.

Steck, M. (Hrsg.): Proklus Diadochus. Euklidkommentar. Deutsche Akademie der Naturforscher, Halle 1945.

Steen, L. A.: Mathematics Today. Springer, New-York, Heidelberg, Berlin 1979.

Toeplitz, O.: Die Entwicklung der Analysis. Wissenschaftliche Buchgesellschaft, Darmstadt 1972.

Viète, F.: Einführung in die Neue Algebra. Übersetzt und erläutert von K. Reich und H. Gericke. W. Fritsch, München 1973.

Vogel, K. (Hrsg.): Chiu-chang suan-chu. Neun Bücher arithmetischer Technik. - (Ostwalds Klassiker, Neue Folge Bd. 4). Vieweg, Braunschweig 1968.

Weigel, E.: Philosophia Mathematica, Theologia Naturalis Solida, Per singulas Scientias continuata, Universae Artis Inveniendis prima Stamina complectens. Matth. Birckner, Jena 1693.

Zimmermann, B.: Heuristische Strategien in der Geschichte der Mathematik. In: Glatfeld 1990.

Zimmermann, B.: Heuristik als ein Element mathematischer Denk- und Lernprozesse. Fallstudien zur Stellung mathematischer Heuristik im Bild von Mathematik bei Lehrern und Schülern sowie in der Geschichte der Mathematik. Habilitationsschrift, Hamburg 1991.

Zimmermann, B. (Hrsg.): Kaleidoskop elementarmathematischen Entdeckens. Franzbecker, Bad Salzdetfurth 1995.

Zimmermann, B. (1995a): Rekonstruktionsversuche mathematischer Denk- und Lernprozesse anhand früher Zeugnisse aus der Geschichte der Mathematik. In: Zimmermann 1995.